This was written back in 2009. Some of the references are out of date, and the insights seem more commonplace now. I can’t tell if that’s because they’ve been borne out by time, or that they were obvious all along.
Backgammon is an ancient game, perhaps the oldest in the world.
Despite the fact that the inner workings of the game – the rules of checker movement – are obviously of human invention, the obscurity of their providence and their sheer simplicity almost makes them akin to natural physical laws, applying themselves to the minimalistic universe of the backgammon board.
Like the physical world, too, backgammon might seem to us to behave as an intractable mixture of determinism and randomness. Reports of games very similar, but presumably genetically unrelated, to backgammon being played by native people in the New World by the first European explorers might suggest that backgammon-like games represent a natural class of game to emerge from the mathematics of probability and position.
Because the study of this world – the science of backgammon – may be pursued for both fun and (gambling) profit, it too has a long history. And curiously, this natural philosophy follows a similar path to investigations of the broader universe.
History of a preferred move
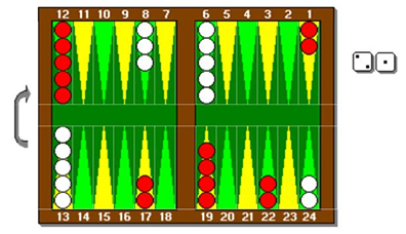
Take this example of (a response to) an opening move. Some opening moves are almost forced, usually because of the absurdity of alternative moves. 2-1 has several viable options, however:
Split runners: 24/23 or 24/22
Drop midpoint: 13/11
Slot board: 6/5
In combinations. Here 24/22 is restricted, so the options are 13/11 combined with either splitting 24/23 or slotting 6/5.
Classical backgammon strategy, played for time immemorial, looks for common sense principles to apply throughout the game. Blots, and shots, should be minimized. Backgammon is a race, and the first to disentangle his back checkers wins. Getting ahead in the race matters more than fancy positional stuff. An understanding of the backgammon world as a whole was what was needed to win the game. This all recommends splitting the back men 24/23 – maximizing their chances of escaping. Slotting the five point is definitely out, because i) it creates an unnecessary blot in your home board which will lose you a lot in the race if hit and ii) the positional value of the five point is not considered to be worth this sort of risk.
Modern backgammon theory developed in the 1970s as a results of a more individual treatment of particular game positions pioneered by Magriel. Instead of general principles to apply to the whole game, various ways to win the game (running, holding, priming, attacking) were identified. Plays that then emphasized one or other of these conclusions, most convenient for the player, are then identified as best – thematic plays. Common aspects of all themes were regarded as particularly important, such as holding your and your opponent’s five point. Combining a good understanding of basic probability (such as duplication) with these thematic plays is suggested to always give the best play. Modern opening theory would prefer slotting with 6/5. The five point is always valuable; you should put your checkers where they belong; you should build up your board as your opponent already has a better board. All these offset the potential loss in the race, which is only one theme in play.
But current practice relies on the ability of new technology to tell us, with a high degree of precision, what the actual best opening play is. By playing through thousands of games following the critical decision with at least human levels of skill, the play that wins the most times can be identified – none of this was possible before sufficient computing power and neural nets became available in the late 1990s.
Computer generated roll-outs indicate that, ironically, the ancient choice of splitting the checkers is in fact better.
Computer generated roll-outs indicate that, ironically, the ancient choice of splitting the checkers is in fact better. Players generally justify moves using various criteria from modern theory. If trusted rollouts indicate that another move is, in fact, preferable, then this move can in turn be justified by adjusting the importance (weighting) given to the different components of modern theory (maybe the race is more important than we suspected in this position).
A comprehensible world
As the sophistication of backgammon theory has increased so has the difficulty of its application.
The initial assumption that the universe of backgammon should be easily comprehended by some basic principles has its parallels in the belief that the universe was made for easy human understanding. An Aristotalean view of the universe, with the Earth at its centre, is intuitive and psychologically compelling: the planets and stars are merely our satellites, maybe reflecting or prefiguring events on Earth.
The truth that our planet is only a smallish one of eight, and that our sun is just another star (and not a special one at that) is jarring and makes our place in the universe difficult to understand. Religious interpretation is obvious: as humans are the only ones with any hope of understanding the universe, and since we are good at understanding macroscopic events in our own lives, surely the universe must have been made with our understanding in mind?
Early science – as the study of an organized God’s universe – also looked for these ways in for intuitive human understanding in a universe that was becoming increasingly complex. To ancient eyes, the movements of the constellations and planets, while clearly ordered, was sufficiently complex to prevent mechanistic understanding: instead they must represent the influence of some great, anthropomorphic will.
Enlightenment technology revealed that instead of being willed, these events appeared to follow very complex, but predictable, patterns. Discovery of these patterns allowed general rules – like gravitation – to be formulated. A great deal of complexity – impossibly to hold in your head and comprehend – could be reduced to some simple principles, which with some mathematical education could be grasped by anyone.
Thus the organization of the universe did follow an anthropic scheme after all – that of the machine.
Thus the organization of the universe did follow an anthropic scheme after all – that of the machine. This reductionism became the core of scientific knowledge: technology revealed more and more detail, which to be understood had to be refined into simple themes which could then be combined to make predictions, often quite accurately.
Reductionism
Despite the unpopularity of the term, until very recently reductionism remained the only systematic way for the extraction of knowledge from very complex natural systems.
Reductionism made the science of biology, as a consistent body of knowledge, possible. Simple, intuitive biology had of course been practiced since ancient times: even when animals were first domesticated the basics of heredity, and hence selective breeding, must have been known.
But to make sense of the cornucopia of life in the world, and being discovered all the time, systematic classification of features; reduction to sets of common factors; was needed. And observation of commonalities between living things leads, eventually, to a realization that they are related – add to this observation of change over time and evolution becomes, in hindsight, obvious.
Common descent is the one great piece of reductionism that makes ordered sense of facts in biology. In fact, “nothing in biology makes sense except in the light of evolution” – a world in which all the forms of life had been dumped, fully formed and exactly as they are now, is considerably more absurd (ie. alien to human comprehension) than one where they have slowly developed from a common ancestor.
In biology, the importance of this shift of allegiances: from where simple comprehensible laws demonstrate a designing anthropic will, to where they seem to argue against it; cannot be overstated.
Non-reductive knowledge
But a further irony is that the apex of technology – the computer, the thinking machine – has given us another way to extract knowledge from the world.
Information, as data, can be taken from the natural world in huge amounts. Computers have the ability to faithfully store and manipulate such large quantities of information. In systems which have been resistant to attack by traditional reductionist methods – they are too complex, have too many exceptions – large-scale analysis of data is another way to gain knowledge. The data can be mined and analysed to try and find traditional reductionist patterns and trends; or can be used to make a model of the natural system in virtual form.
We can then ask the computer how the system behaves under particular circumstances or if perturbed in certain ways. If we can extract enough data from the natural system, then we lose the need for any generalised, reductive laws to predict outcomes – we simply pull the correct (or interpolated) value out of the computer.
Whether we, or the computer, really have “knowledge” of the natural system is an interesting philosophical question.
Perfect Backgammon
Because the universe of backgammon is so simple, extraction of information into a computer and automated analysis can almost reach completion. In this case the information takes the form of which is the best play under each individual situation.
Because of the indeterminism of the game and large number of position combinations, it is computationally impossible to simply database the best moves under all circumstances. Instead, some generalization is required by the computer itself – reductionism of an electronic sort in a neural net. By making computer programs play each other for millions of games, a system of weightings can be empirically determined which make the neural net play extremely well.
Despite the fact the computer has “learnt” to play based on generalization, these generalisations are themselves so complex that humans could never themselves learn to use them to improve their own play: in effect the neural net weights are a natural consequence of the system itself, an emergent quality that becomes obvious upon sufficient observation (understanding is not required).
How good are the programs? As of 2009, even modest computing power is enough to play a world-beating game.
Now the computers have taken their observations from the backgammon universe and performed their level of processing upon them, just like our models of the real world we can ask them questions and expect accurate answers.
Which is the best opening move in the problem above? The computer will play through thousands of virtual games, starting from each opening move, as a sample of all possible games of backgammon. When enough games have been played to minimize the effects of chance we will have an answer as to which play will win more often.
How confident are we that this is absolutely the best move? Early neural nets often had blind spots and odd quirks, easily identified absurd plays. But a net like GNUBG can play every move better than a world-class player, and can then eliminate the element of chance in the roll-out. An entire game based on the results of roll-outs would be indistinguishable, in human terms, from perfect backgammon.
Backgammon without theory
The advent of these modern programs has had an interesting influence on backgammon strategy. We now have an argument settler: generally the result of an intensive rollout is accepted by everyone as the best move.
But changing a long-accepted play as a result of computation does not necessarily add to understanding.
But changing a long-accepted play as a result of computation does not necessarily add to understanding. Simple rules, strategies and themes are needed to understand the game on human terms. Some players are capable of prodigious calculation, allowing them to mathematically rationalize their moves – but then again, many of the top players don’t even bother to count shots. You can play a surprisingly competent game of backgammon by just making the most aesthetically pleasing move.
You can improve your game a huge amount by playing against the bots, but in the absence of understanding the theme-based systems of modern theory your improvement will plateau.
The upshot of all this is that top players justify their moves based on the many sensible systems of modern theory; and then amend this justification if a roll-out shows it to be significantly wrong. Without an intuitive feel of why a play was right, this can make it difficult for beginners and intermediate players to see how you are supposed to arrive at the right move – without help from the machine – at all.
Natural science as performed by computer
So which system – the computer’s observation derived neural net, or the humanistic system of interlocking rules and themes – best represent the miniature natural universe of backgammon?
In terms of quality of play – winning games – the computer is now winning out over the human more and more convincingly. But who has greater understanding? Without question, the human.
The rules and interpretations Magriel put on the game thirty years ago may be approximate and subject to exceptions, but they allow us to play and enjoy the game in our human element, despite the fact the game is often counter-intuitive and chaotic. Because the patterns we impose to play the game have to be simple to allow us to remember and apply them, they must also be deeper and more general for them to work as effective strategies.
We could have built the neural nets, and trained them to play backgammon extremely well, without ever having played a single game of backgammon ourselves. If aliens some time challenged us to an intergalactic chouette, we could have given them a damn good run for their money and still be completely ignorant of even the simplest strategies in the game. The aliens may have left, considering the computers to be the wisest organisms on the planet and us simple button-pushers and electricity-providers.
This has implications for computerization of science in general. Of course the neural nets have been an asset to backgammon, and a huge amount has been learnt in their building and use. The way they are used is as a complement to human understanding of the game, and as such they are only useful. But in some aspects of science we move closer to building knowledge algorithms for processes which we have very little understanding of.